Part1 线性动态规划

P2679 [NOIP 2015 提高组] 子串

很有手法的一道动态规划。考虑用四维dp[i][j][k][v]来进行动态规划。dp[i][j][k][v]表示当a串到第i位时，b串已经匹配到了第j位，同时使用了k个子串，并且a[i]这个字符是否使用了（v=0表示没有用，1表示用了）。那么存在两种情况：a[i]==b[j] a[i]!=b[j] 每种情况又分使用a[i]和不实用a[i]两种情况，总共的动态转移方程就有四种情况：

下面详细解释一下为什么要这样进行转移：

当a[i]==b[j]时，如果选了a[i]，那么可以肯定a[i-1]匹配到了b[j-1]。那么如果dp[i-1][j-1]也使用了p个子串，那么可以肯定a[i-1]和a[i]是连在一起的，a[i-1]也必须得选上，因此加上dp[i-1][j-1][p][1]。假如dp[i-1]dp[j-1]只使用了p-1个子串，那么这个时候有两种情况，a[i-1]选上了与没选上，因此加上这两种情况。从前一个状态转移到后一个状态时，p只可能+1或者不加，因此只有p和p-1两种可能。 再看没选a[i]：没选a[i]匹配到了b[j]，那么a[i-1]也匹配到了b[j]。没选a[i]此时用了p个子串，那么dp[i-1][j]也用了p个子串，因此只有两种可能了，a[i-1]与b[j]匹配上 和 a[i-1]与b[j]没匹配上，因此加上这两种可能的情况数。

如果a[i]!=b[j]，那么a[i]就不可能被选上，因此dp[i][j][k][1]=0；如果a[i]没选上，和上面没选上的情况一样，加上这两种情况。

当然，通过状态转移方程发现，每一个i只用到了i-1，因此可以把i给滚动，降低了一千倍空间复杂度。下面贴上AC代码：

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int mod = 1000000007;

int n, m, c;
int dp[2][205][205][2];
char a[1005], b[205];

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin >> n >> m >> c;

	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	for (int i = 1; i <= m; i++) {
		cin >> b[i];
	}
	int val = 1;
	dp[0][0][0][0] = 1;
	dp[1][0][0][0] = 1;
	for (int i = 1; i <= n; i++, val ^= 1) {
		for (int j = 1; j <= m; j++) {
			for (int k = 1; k <= c; k++) {
				if (a[i] == b[j]) {
					dp[val][j][k][1] = ((dp[val ^ 1][j - 1][k][1] + dp[val ^ 1][j - 1][k - 1][1]) % mod + dp[val ^ 1][j - 1][k - 1][0]) %
					                   mod;
					dp[val][j][k][0] = (dp[val ^ 1][j][k][0] + dp[val ^ 1][j][k][1]) % mod;
				} else {
					dp[val][j][k][1] = 0;
					dp[val][j][k][0] = (dp[val ^ 1][j][k][0] + dp[val ^ 1][j][k][1]) % mod;
				}
			}
		}
	}
	cout << (dp[n & 1][m][c][1] + dp[n & 1][m][c][0]) % mod;
	return 0;
}

P1216 [IOI 1994] 数字三角形 Number Triangles

这题最开始想的是用一维dp，dp[i]表示到第i行路径最大的值，后面发现好像不行，因为dp[i+1]并不是完全取决于dp[i]，还跟前后两行位置关系有关。因此考虑使用二维dp，dp[i][j]表示走到第i行j列经过数字最大和。dp[i][j]就等于dp[i-1][j-1]和dp[i-1][j]之中最大值加上当前位置的值，因为dp[i][j]只能从这两个位置来。最后遍历一遍dp数组的第n行，找到最大值OK了。

#include <bits/stdc++.h>
using namespace std;

int arr[1005][1005];
int n;
int dp[1005][1005];

int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= i; j++) {
			cin >> arr[i][j];
		}
	}
	dp[1][1] = arr[1][1];
	for (int i = 2; i <= n; i++) {
		for (int j = 1; j <= i; j++) {
			dp[i][j] = max(dp[i - 1][j - 1], dp[i - 1][j]) + arr[i][j];
		}
	}
	int mx = 0;
	for (int i = 1; i <= n; i++) {
		mx = max(mx, dp[n][i]);
	}
	cout << mx;
	return 0;
}

P1020 [NOIP 1999 提高组] 导弹拦截

这道题其实是一道最长上升（不降）子序列和最长下降（不升）子序列的模版题。一个序列中，最长上升子序列的长度=能分成的最少的不升子序列的个数。第一问求最长不升子序列长度，第二问求最长上升子序列长度。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int syb[100005], arr[100005];
int mx = 0, sz = 0;

void getnum() {
	int a = 0;
	char c;
	while (c = getchar()) {
		if (isdigit(c)) {
			a = a * 10 + c - '0';
		} else if (c == ' ') {
			sz++;
			arr[sz] = a;
			a = 0;
		} else {
			sz++;
			arr[sz] = a;
			break;
		}
	}
}

int main() {
	getnum();

	syb[1] = arr[1];
	int msz = 1;
	for (int i = 2; i <= sz; i++) {
		auto it = upper_bound(syb + 1, syb + 1 + msz, arr[i], greater<int>());
		if (it == syb + 1 + msz) {
			msz++;
			syb[msz] = arr[i];
		} else {
			*it = arr[i];
		}
	}
	cout << msz << endl;
	memset(syb, 0, sizeof(syb));
	syb[1] = arr[1];
	msz = 1;
	for (int i = 2; i <= sz; i++) {
		auto it = lower_bound(syb + 1, syb + 1 + msz, arr[i]);
		if (it == syb + 1 + msz) {
			msz++;
			syb[msz] = arr[i];
		} else {
			*it = arr[i];
		}
	}
	cout << msz << endl;
	return 0;
}

P1091 [NOIP 2004 提高组] 合唱队形

在序列中找到一个位置i，使得从序列开始到i的上升子序列和i到序列结束的下降子序列总的元素最大。因此这道题本质还是求最长上升子序列，最长下降子序列。这道题数据量比较小，可以用O(n*2)的方法做，但这里还是用O(nlogn)的方法

#include <bits/stdc++.h>
using namespace std;

int left_dp[105], right_dp[105];
int arr1[105], arr2[105]; 
int d1[105], d2[105]; 

int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> arr1[i];
        arr2[n - i + 1] = arr1[i]; 
    }

    int len1 = 0;
    for (int i = 1; i <= n; i++) {
        auto it = lower_bound(d1 + 1, d1 + 1 + len1, arr1[i]);
        int pos = it - d1;
        
        if (pos > len1) {
            d1[++len1] = arr1[i];
            left_dp[i] = len1;
        } else {
            *it = arr1[i];
            left_dp[i] = pos;
        }
    }

    int len2 = 0;
    for (int i = 1; i <= n; i++) {
        auto it = lower_bound(d2 + 1, d2 + 1 + len2, arr2[i]);
        int pos = it - d2;
        
        if (pos > len2) {
            d2[++len2] = arr2[i];
            right_dp[i] = len2;
        } else {
            *it = arr2[i];
            right_dp[i] = pos;
        }
    }
    // 寻找最佳分割点
    int max_len = 0;
    for (int i = 1; i <= n; i++) {
        int j = n - i + 1;
        max_len = max(max_len, left_dp[i] + right_dp[j] - 1);
    }

    cout << n - max_len << endl;
    return 0;
}

P1095 [NOIP 2007 普及组] 守望者的逃离

对于这道题，使用fla和run两个变量来维护两种距离。如果以7秒钟为周期，蓄力五秒flash两次，那么能够跑120米；单纯跑7秒跑119米。因此flash比run快，甚至开局还有多余的蓝。变量fla记录纯flash的距离，run记录纯跑的距离。每一秒结束后，如果fla比run大，那么把run更新为fla的距离。一道简单的动态规划。

#include <bits/stdc++.h>
using namespace std;

int run = 0, fla = 0;
int m, s, t;


int main() {
	cin >> m >> s >> t;
	for (int i = 1; i <= t; i++) {
		if (m >= 10) {
			fla += 60;
			run += 17;
			m -= 10;
		} else {
			m += 4;
			run += 17;
		}
		run = max(run, fla);
		if (run >= s) {
			cout << "Yes" << endl << i;
			return 0;
		}
	}
	cout << "No" << endl << run;
	return 0;
}

P1541 [NOIP 2010 提高组] 乌龟棋

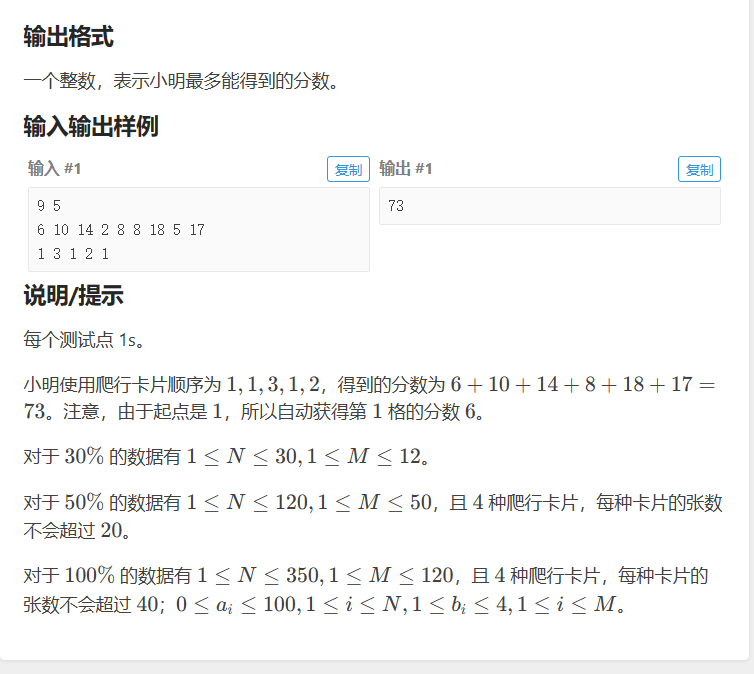
这道题第一想法就是把dp[i]当做到第i个格子时最大的得分来动态规划，但是这样做的话就要考虑到这个格子是否可达，达到这个格子有哪些方法都要考虑进去，很复杂不好做。实际上题目中给出所有的牌用完之后刚好能到达终点，并且我们可以通过已经用掉了哪些牌来确定当前位置在哪，可以用一个四维数组来动态规划，dp[a][b][c][d]来表示用了a张第一种牌、b张第二种牌……时最大的得分，可以很容易的知道dp[a][b][c][d]由dp[a-1][b][c][d]、dp[a][b-1][c][d]、dp[a][b][c-1][d]、dp[a][b][c][d-1]的最大值加上当前abcd的位置上的得分而来。最后输出dp每种牌最大数量（即终点）就OK了

#include <bits/stdc++.h>
using namespace std;

int n, m;
int arr[355], ka[5];
int dp[45][45][45][45]; // 维度大小根据卡片最大数量(40)设置

int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		cin >> arr[i];
	}
	int temp;
	memset(ka, 0, sizeof(ka)); // 初始化卡片计数
	for (int i = 1; i <= m; i++) {
		cin >> temp;
		ka[temp]++;
	}
	dp[0][0][0][0] = arr[1];
	for (int a = 0; a <= ka[1]; a++) {
		for (int b = 0; b <= ka[2]; b++) {
			for (int c = 0; c <= ka[3]; c++) {
				for (int d = 0; d <= ka[4]; d++) {
					int pos = 1 + a + 2 * b + 3 * c + 4 * d;
					int max_val = -1;
					if (a > 0)
						max_val = max(max_val, dp[a - 1][b][c][d]);
					if (b > 0)
						max_val = max(max_val, dp[a][b - 1][c][d]);
					if (c > 0)
						max_val = max(max_val, dp[a][b][c - 1][d]);
					if (d > 0)
						max_val = max(max_val, dp[a][b][c][d - 1]);
					if (max_val != -1) {
						dp[a][b][c][d] = max_val + arr[pos];
					}
				}
			}
		}
	}
	cout << dp[ka[1]][ka[2]][ka[3]][ka[4]] << endl;
	return 0;
}

P1868 饥饿的奶牛

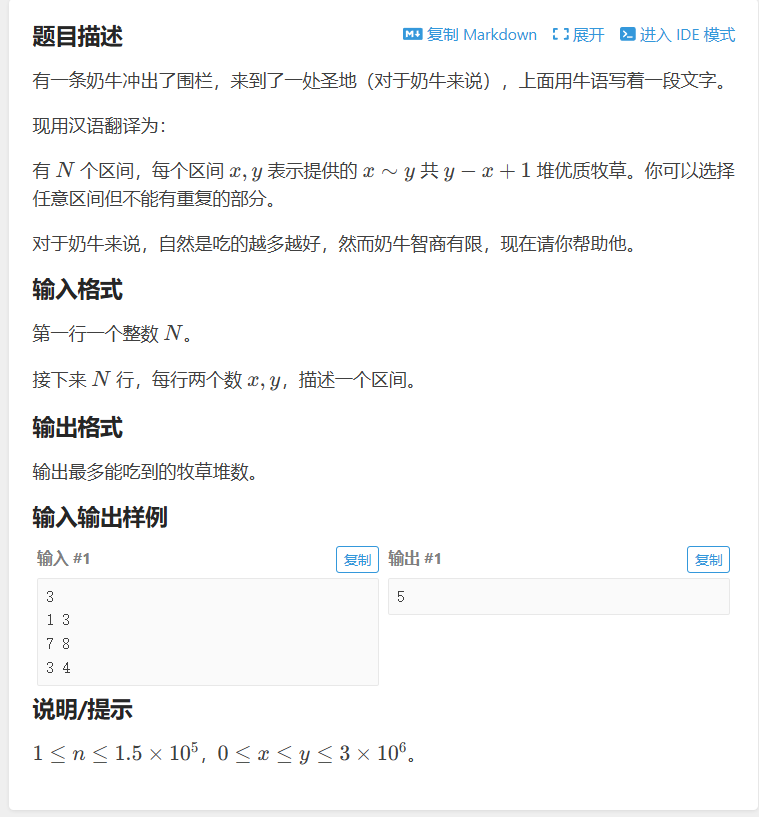
一个区间最值问题，可以考虑用dp[i]来表示到第i格时能吃到的最多的草，最后结果是dp[给出的最右端点]关于状态转移，如果当前的i不存在以i结尾的区间，那么dp[i]=dp[i-1]；如果存在，假设这个区间左端点是left，那么就对比dp[i-1]和dp[left-1]+区间值。用大值更新dp[i]。

考虑用一个pair<int,int>数组来记录给出的每个区间，然后通过arr[i].second的大小来对arr进行sort升序排序。用mx变量维护最大的右端点，初始化dp[0]=0，然后对dp[i]进行从1到mx的遍历。具体代码如下：

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int n;
pair<int, int> arr[250005];
ll dp[3000005];

bool cmp(const pair<int, int> &a, const pair<int, int> &b) {
	return a.second < b.second;
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin >> n;
	int mx = 0;
	for (int i = 1; i <= n; i++) {
		cin >> arr[i].first >> arr[i].second;
		mx = max(mx, arr[i].second);
	}
	sort(arr + 1, arr + 1 + n, cmp);
	dp[0] = 0;
	int sid = 1;

	for (int i = 1; i <= mx; i++) {
		dp[i] = dp[i - 1];
		if (i != arr[sid].second) {
			continue;
		}
		while (i == arr[sid].second && sid <= n) {
			dp[i] = max(dp[i], dp[arr[sid].first - 1] + arr[sid].second - arr[sid].first + 1);
			sid++;
		}

	}
	cout << dp[mx] << endl;
	return 0;
}

P3558 [POI 2013] BAJ-Bytecomputer

很牛逼的一道动态规划，完全理解起来不是很容易。代码借鉴题解中一位大佬的，很牛逼的压缩，很牛逼的思路，希望暑假结束后我也能达到这样的水平。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int n;
int f[3];
int inf = 1 << 27;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin >> n;
	int temp;
	cin >> temp;
	memset(f, 63, sizeof(f));
	f[temp + 1] = 0;

	for (int i = 2; i <= n; i++) {
		cin >> temp;
		if (temp == -1) {
			f[1] = inf;
			f[2] += 2;
		} else if (temp == 0) {
			f[1] = min(f[0], f[1]);
			f[0]++;
			f[2]++;
		} else {
			f[2] = min(f[0], min(f[1], f[2]));
			f[1] = f[0] + 1;
			f[0] += 2;
		}
	}
	int temp1 = min(f[0], min(f[1], f[2]));
	if (temp1 >= inf) {
		cout << "BRAK";
	} else {
		cout << temp1;
	}
	return 0;
}

P4158 [SCOI2009] 粉刷匠

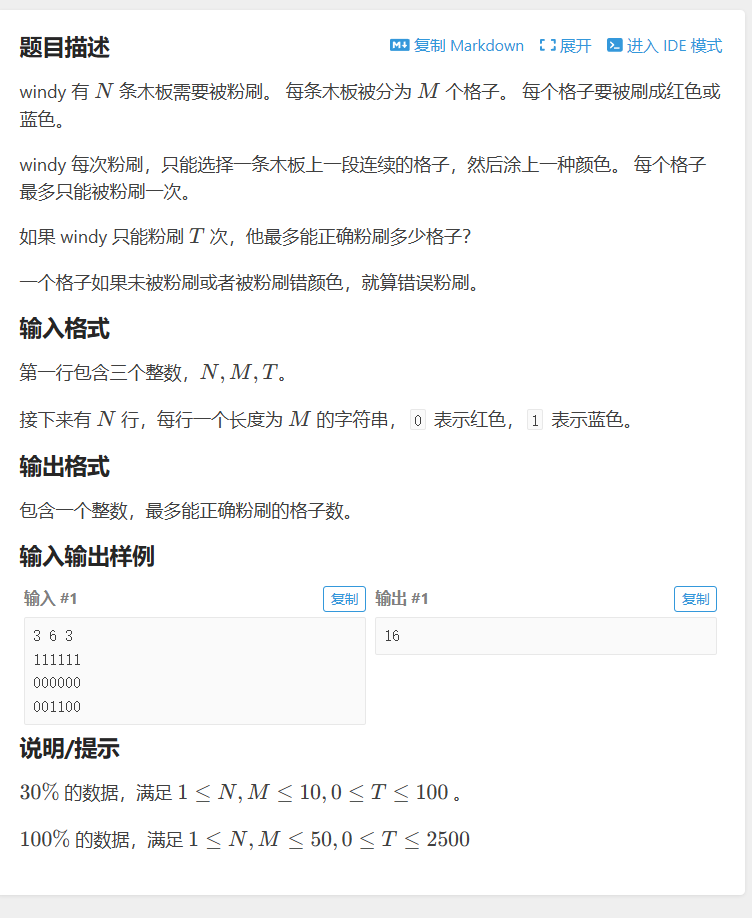
第一次没看题解过的蓝题。讲一下我的思考过程。这道题分为两个动态规划的过程，也有点背包dp的意思。

状态表示：用dp[i][j]来表示前面i行总共用了j次机会得到的最大值。那么想当然dp[i][j]就等于 (dp[i-1][j-x]加上第i行花费x次得到的最大值)中的最大值。因此就得知道第i行用x次能得到的最大值是多少，这里也是一层动态规划。

先来说一下怎么第i行用x次能得到的最大值是多少。首先用一个数组f[i][j][k]来表示第i行从j列到k列，0或1总数的较大值，实际上就是从j到k只刷一次的值。这个很好求，用暴力就可以了。然后用一个数组d[i][j][k]用来表示第i行前j列用了k次机会的最大值，可以知道d[i][j][k]=f[i][x][j]+d[i][x-1][k-1]的最大值。这样一来d函数就求完了。

接下来给dp数组初始化，把d[1][m][x]赋值给给dp[i][x]。之后从第二行进行dp数组的动态规划。最后输出dp[n][min(t,n*m)]就好了。代码如下：

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int n, m, t;
int f[55][55][55];
int d[55][55][55];
int dp[55][2505];
char arr[55][55];

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin >> n >> m >> t;
	int num = min(m, t);
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			cin >> arr[i][j];
		}
	}
	int temp0, temp1;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			temp0 = 0, temp1 = 0;
			for (int k = j; k <= m; k++) {
				if (arr[i][k] == '0') {
					temp0++;
				} else {
					temp1++;
				}
				f[i][j][k] = max(temp0, temp1);
			}
		}
	}

	for (int i = 1; i <= n; i++) {

		for (int j = 1; j <= m; j++) {
			d[i][j][1] = f[i][1][j];
		}

		for (int k = 2; k <= num; k++) {
			for (int j = k; j <= m; j++) {
				int temp = 0;
				for (int l = j; l >= k; l--) {
					temp = max(temp, d[i][l - 1][k - 1] + f[i][l][j]);
				}
				d[i][j][k] = temp;
			}
		}
	}

	for (int i = 1; i <= num; i++) {
		dp[1][i] = d[1][m][i];
	}
	int temp, mx;
	for (int i = 2; i <= n; i++) {
		mx = min(t, i * m);
		for (int k = 1; k <= mx; k++) {
			temp = 0;
			for (int p = 0; p <= min(mx, m); p++) {
				temp = max(temp, d[i][m][p] + dp[i - 1][k - p]);
			}
			dp[i][k] = temp;
		}
	}
	mx = min(t, n * m);
	cout << dp[n][mx];

	return 0;
}

P3336 [ZJOI2013] 话旧

我的第一道黑题，借鉴了大佬们的题解。以后一定能自己写出很多很多道黑题！

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

const ll mod = 19940417;
const int MAXK = 1000010;

struct Point {
	int x, y;
};

bool operator<(const Point &a, const Point &b) {
	return a.x < b.x;
}

bool operator==(const Point &a, const Point &b) {
	return a.x == b.x;
}
Point p[MAXK];
ll f[MAXK][2];

ll qpow(ll a, ll b) {
	ll ret = 1;
	while (b) {
		if (b % 2)
			ret = ret * a % mod;
		b /= 2;
		a = a * a % mod;
	}
	return ret;
}

inline void add(ll &x, ll y) {
	x = (x + y % mod) % mod;
}

int main() {
	int n, k, tmax = 0;
	scanf("%d%d", &n, &k);
	p[k + 1].x = n;
	for (int i = 1; i <= k; i++)
		scanf("%d%d", &p[i].x, &p[i].y);
	sort(p, p + k + 2);
	k = unique(p, p + k + 2) - p - 1;
	f[0][1] = 1;
	for (int i = 1; i <= k; i++) {
		int x1 = p[i - 1].x, y1 = p[i - 1].y;
		int x2 = p[i].x, y2 = p[i].y;
		int len = x2 - x1 - y1 - y2;
		
		if (x1 - x2 == y1 - y2) {
			add(f[i][0], f[i - 1][0]);
			if (y1 == 0)
				add(f[i][0], f[i - 1][1]);
		} else if (x1 - x2 == y2 - y1) {
			add(f[i][1], f[i - 1][0] + f[i - 1][1]);
		} else if (len < 0) {
			add(f[i][1], f[i - 1][0]);
			if (y1 == 0)
				add(f[i][1], f[i - 1][1]);
		} else if (len == 0) {
			add(f[i][1], f[i - 1][0]);
			if (y1 == 0)
				add(f[i][1], f[i - 1][1]);
			add(f[i][0], f[i - 1][0] + f[i - 1][1]);
		} else {
			ll t = (2 * f[i - 1][0] + f[i - 1][1]) * qpow(2, len / 2 - 1) % mod;
			if (y2 > 0)
				add(f[i][0], t);
			add(f[i][1], t);
		}
		if(f[i][1]>0){
			tmax = max(tmax, x2 - x1 + y1 + y2);
		}
	}
	printf("%lld %d\n", f[k][1], tmax / 2);
	return 0;
}

Part2 背包动态规划

P1048 [NOIP 2005 普及组] 采药

实际上就是01背包的模版题，换了一个题目背景。这里贴一下二维dp和一维dp的做法

二维：

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int t, m;
int dp[105][1005];
pair<int, int> arr[105];

int main() {
	cin >> t >> m;
	for (int i = 1; i <= m; i++) {
		cin >> arr[i].first >> arr[i].second;
	}
	for (int i = 1; i <= m; i++) {
		for (int j = 1; j <= t; j++) {
			if (j >= arr[i].first) {
				dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - arr[i].first] + arr[i].second);
			} else {
				dp[i][j] = dp[i - 1][j];
			}

		}
	}
	cout << dp[m][t] << endl;
	return 0;
}

一维

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int t, m;
int dp[1005];
pair<int, int> arr[105];

int main() {
	cin >> t >> m;
	for (int i = 1; i <= m; i++) {
		cin >> arr[i].first >> arr[i].second;
	}
	for (int i = 1; i <= m; i++) {
		for (int j = t; j >= 1; j--) {
			if (j >= arr[i].first) {
				dp[j] = max(dp[j - arr[i].first] + arr[i].second, dp[j]);
			}

		}
	}
	cout << dp[t] << endl;
	return 0;
}

P1060 [NOIP 2006 普及组] 开心的金明

还是一道01背包，唯一的变化是要对物品的价值做一下处理

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int n, m;
int dp[30005];
pair<int, int> arr[30];

int main() {
	cin >> n >> m;
	int temp;
	for (int i = 1; i <= m; i++) {
		cin >> arr[i].first >> temp;
		arr[i].second = temp * arr[i].first;
	}
	for (int i = 1; i <= m; i++) {
		for (int j = n; j >= 0; j--) {
			if (j >= arr[i].first) {
				dp[j] = max(dp[j], dp[j - arr[i].first] + arr[i].second);
			}
		}
	}
	cout << dp[n];
	return 0;
}

P1855 榨取kkksc03

从01背包（只有一个背包，即只有一种资本）变成了多维背包，这题是二维背包，拥有两个背包。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int n, m, t;
int dp[205][205];
pair<int, int> arr[105];

int main() {
	cin >> n >> m >> t;
	for (int i = 1; i <= n; i++) {
		cin >> arr[i].first >> arr[i].second;
	}
	for (int i = 1; i <= n; i++) {
		for (int j = m; j >= 0; j--) {
			for (int k = t; k >= 0; k--) {
				if (j >= arr[i].first && k >= arr[i].second) {
					dp[j][k] = max(dp[j][k], dp[j - arr[i].first][k - arr[i].second] + 1);
				}
			}
		}
	}
	cout << dp[m][t];
	return 0;
}

P5020 [NOIP 2018 提高组] 货币系统

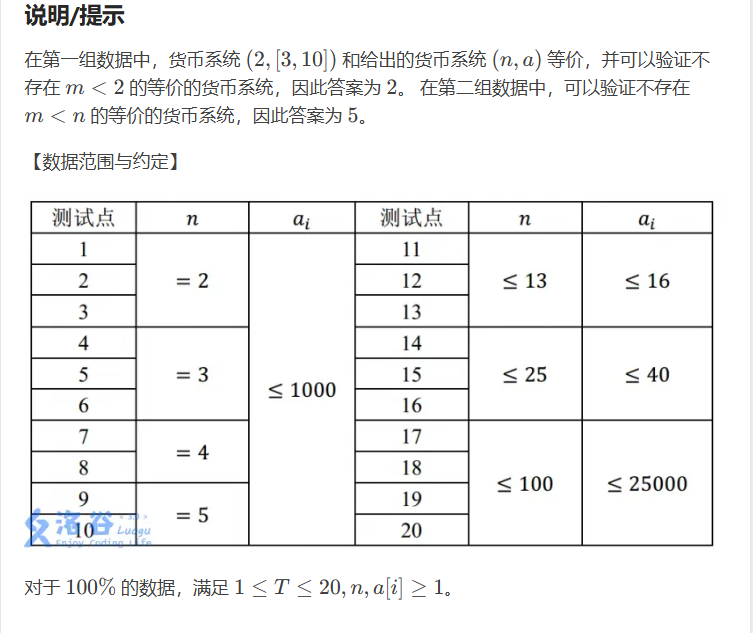
一道完全背包的题。将原来集合中所有能被其它数字组成的数都删去，剩下元素的个数就是要输出的值。因此对面值进行排序，从最小的面值开始遍历，并且遍历当前面值后面的所有值进行凑值。AC代码如下：

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

const int maxdp = 25005;
const int maxn = 105;
int n, t, ans;
int f[maxdp];
int a[maxn];

int main() {
	scanf("%d", &t);
	while (t--) {
		memset(f, 0, sizeof(f));
		scanf("%d", &n);
		ans = n;
		for (int i = 1; i <= n; i++) {
			scanf("%d", &a[i]);
		}
		sort(a + 1, a + n + 1);
		f[0] = 1;
		for (int i = 1; i <= n; i++) {
			if (f[a[i]]) {
				ans--;
				continue;
			}
			for (int j = a[i]; j <= a[n]; j++) {
				f[j] = f[j] | f[j - a[i]];
			}
		}
		printf("%d\n", ans);
	}

	return 0;
}

P1757 通天之分组背包

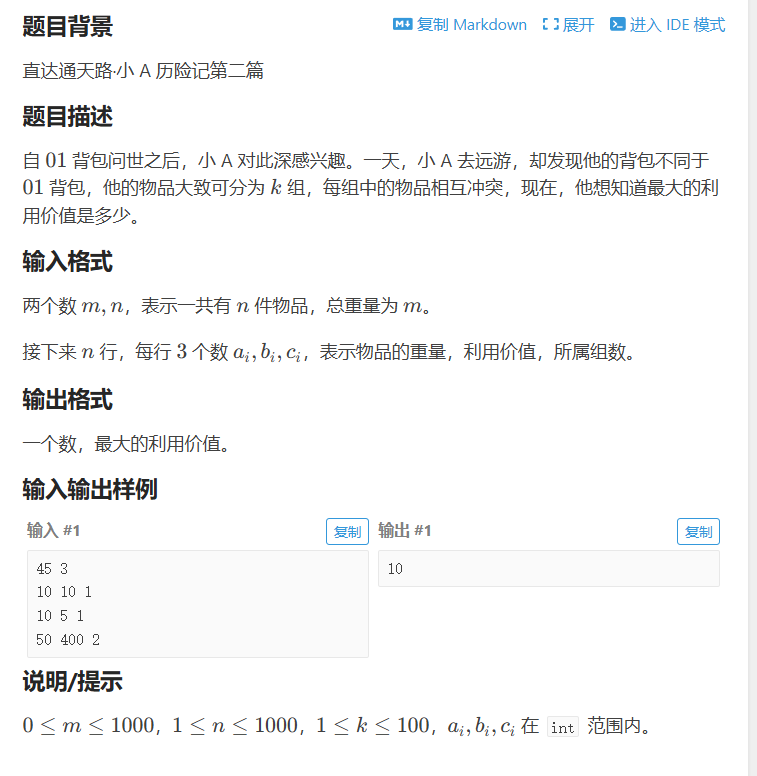
如题名，分组背包的板子题。比较复杂的点在于记录分组与每个分组物品对应的编号

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int n, m;
int w[1005], v[1005], b[1005], g[1005][1005], dp[1005];

int main() {
	cin >> m >> n;
	int temp;
	int t = 0;
	for (int i = 1; i <= n; i++) {
		cin >> w[i] >> v[i] >> temp;
		t = max(t, temp);
		b[temp]++;
		g[temp][b[temp]] = i;
	}
	for (int i = 1; i <= t; i++) {
		for (int j = m; j >= 0; j--) {
			for (int k = 1; k <= b[i]; k++) {
				if (j >= w[g[i][k]]) {
					dp[j] = max(dp[j], dp[j - w[g[i][k]]] + v[g[i][k]]);
				}
			}
		}
	}
	cout << dp[m];
	return 0;
}

P1064 [NOIP 2006 提高组] 金明的预算方案

每一组物品必须选择主项，才能再选择副项，因此对于每一组物品，总共有五种选择情况：1.不选择该组2.选择主项3.选择主项和第一个副项4.选择主项和第二个副项5.选择主项和两个副项。按照每一组进行背包dp

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int n, m;
int w[65][3], v[65][3], b[65], dp[30005];

int main() {
	cin >> n >> m;
	int temp1, temp2, temp3;
	for (int i = 1; i <= m; i++) {
		cin >> temp1 >> temp2 >> temp3;
		if (temp3 == 0) {
			b[i] = 1;
			w[i][0] = temp1;
			v[i][0] = temp2;
		} else {
			if (w[temp3][1] == 0) {
				w[temp3][1] = temp1;
				v[temp3][1] = temp2;
			} else {
				w[temp3][2] = temp1;
				v[temp3][2] = temp2;
			}
		}
	}

	for (int i = 1; i <= m; i++) {
		if (!b[i]) {
			continue;
		}
		for (int j = n; j >= 0; j--) {
			if (j >= w[i][0] + w[i][1] + w[i][2]) {
				dp[j] = max(dp[j], dp[j - w[i][0] - w[i][1] - w[i][2]] + w[i][0] * v[i][0] + w[i][1] * v[i][1] + w[i][2] * v[i][2]);
			}
			if (j >= w[i][0] + w[i][1]) {
				dp[j] = max(dp[j], dp[j - w[i][0] - w[i][1]] + w[i][0] * v[i][0] + w[i][1] * v[i][1]);
			}
			if (j >= w[i][0] + w[i][2]) {
				dp[j] = max(dp[j], dp[j - w[i][0] - w[i][2]] + w[i][0] * v[i][0] + w[i][2] * v[i][2]);
			}
			if (j >= w[i][0]) {
				dp[j] = max(dp[j], dp[j - w[i][0]] + w[i][0] * v[i][0]);
			}
		}
	}
	cout << dp[n];
	return 0;
}

P2946 [USACO09MAR] Cow Frisbee Team S

题目标签是背包dp，虽然说背包dp也是线性dp的一种，但我感觉更像标准的线性dp。

状态表示：用dp[i][j]来表示前i个奶牛中以j为余数的总组合数。假设当前第i个奶牛的能力值是x，那么想要求到第i个奶牛的时候余数为j的组合数，就要知道前面i-1个奶牛余数是 (j+f-x)%f 的组合数。特别的，当前奶牛能力值就是j时，还要再加1，因为本身也是一个组合。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

const int mod = 1e8;
int n, f;
int arr[2005];
int dp[2005][1005];

int main() {
	cin >> n >> f;
	int temp;
	for (int i = 1; i <= n; i++) {
		cin >> temp;
		arr[i] = temp % f;
	}


	for (int i = 1; i <= n; i++) {
		dp[i][arr[i]] += 1;
		for (int j = 0; j < f; j++) {
			dp[i][j] += (dp[i - 1][(j + f - arr[i]) % f] + dp[i - 1][j]) % mod ;
		}

	}
	cout << dp[n][0];
	return 0;
}

P5322 [BJOI2019] 排兵布阵

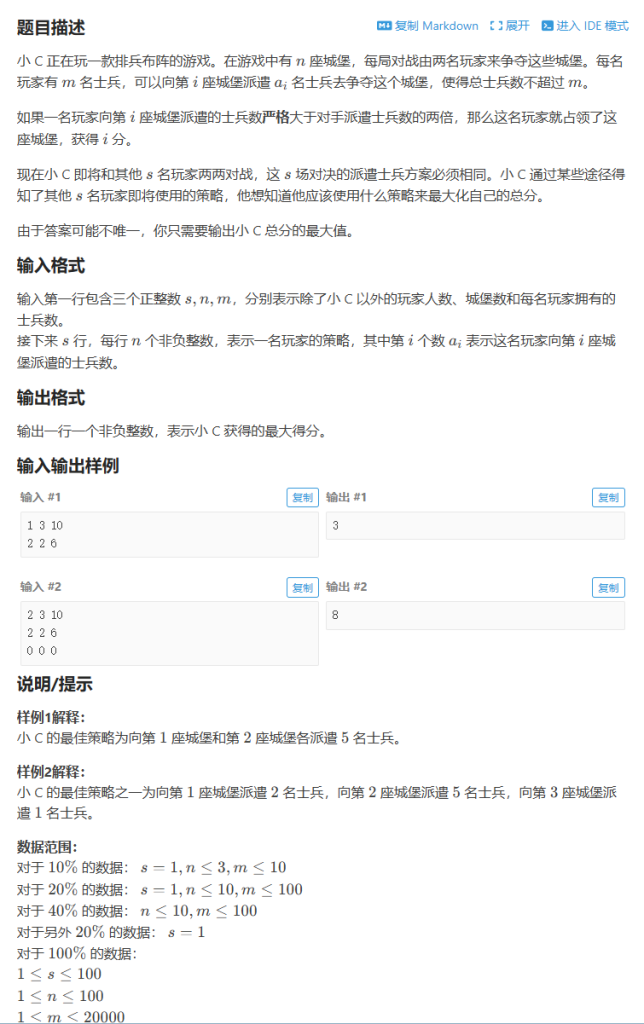
每个城堡是一个物品，士兵数是背包容量，和01背包不同的是，01背包直接减去容量换取得分，但是这道题是分配不同的容量，拿到不同的得分，因此这题需要再加一个内层循环去遍历容量的取值，而容量的取值取决于当前城堡每个其他玩家派遣的数目，根据这个来确定。AC代码如下

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int s, n, m;
int  dp[20005], tar[105][105];

int main() {
	cin >> s >> n >> m;

	for (int i = 1; i <= s; i++) {
		for (int j = 1; j <= n; j++) {
			cin >> tar[j][i];
		}
	}
	for (int i = 1; i <= n; i++) {
		sort(tar[i] + 1, tar[i] + 1 + s);
	}

	int temp;
	for (int i = 1; i <= n; i++) {
		for (int j = m; j >= 0; j--) {
			for (int k = 1; k <= s; k++) {
				temp = tar[i][k] * 2 + 1;
				if (j >= temp) {
					dp[j] = max(dp[j], dp[j - temp] + k * i);
				}
			}
		}
	}
	cout << dp[m];
	return 0;
}

P1156 垃圾陷阱

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int dis, n;

struct rbs {
	int t;
	int h;
	int f;
} rb[110]; 
int f[110], ti[110];

bool cmp(rbs a, rbs b) {
	return a.t < b.t;
}

int main() {
	cin >> dis >> n;
	for (int i = 1; i <= n; i++) {
		cin >> rb[i].t >> rb[i].f >> rb[i].h;
	}
	sort(rb + 1, rb + 1 + n, cmp);
	f[0] = 10;
	for (int i = 1; i <= n; i++) {
		for (int j = dis; j >= 0; j--) {
			if (f[j] >= rb[i].t) {
				if (j + rb[i].h >= dis) {
					cout << rb[i].t << endl; 
					return 0;
				}
				f[j + rb[i].h] = max(f[j + rb[i].h], f[j]);
				f[j] += rb[i].f;
			}
		}
	}
	cout << f[0] << endl; 
	return 0;
}

Part3 区间动态规划

区间动态规划，就是以区间作为动态规划的阶段。

P1880 [NOI1995] 石子合并

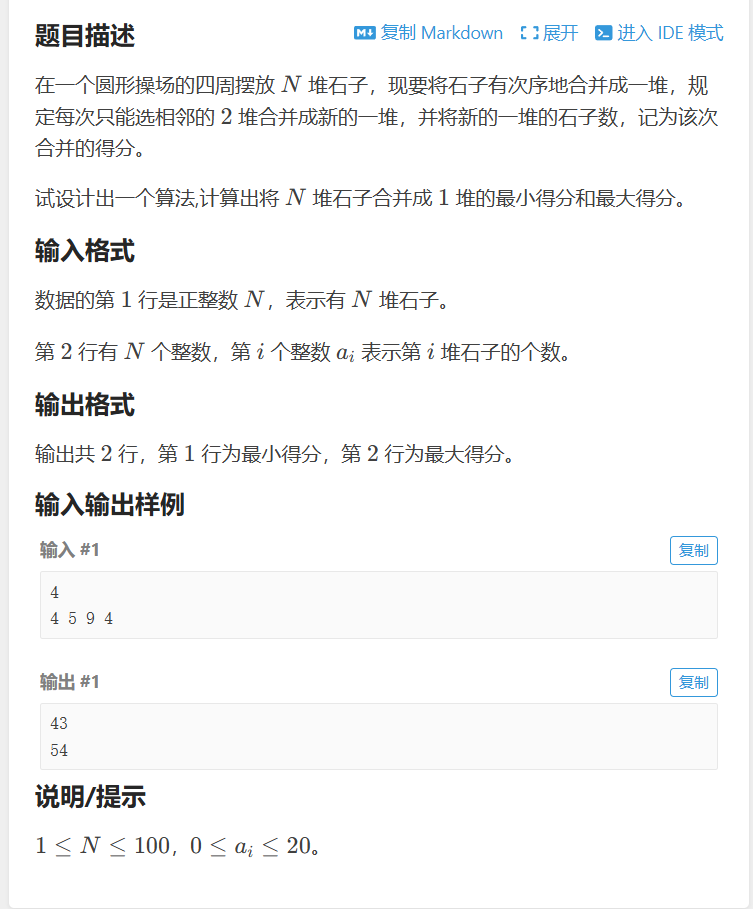
#include <bits/stdc++.h>
using namespace std;

const int INF = 1e9;
int n, arr[205], sum[205], dpm[205][205], dpx[205][205];

int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> arr[i];
		arr[i + n] = arr[i]; // 环形展开
	}
	for (int i = 1; i <= 2 * n; i++)
		sum[i] = sum[i - 1] + arr[i]; // 正确计算前缀和

	// 初始化DP
	for (int len = 1; len <= n; len++) {
		for (int i = 1; i + len - 1 <= 2 * n; i++) {
			int j = i + len - 1;
			if (len == 1) {
				dpm[i][j] = 0;
				dpx[i][j] = 0;
			} else {
				dpm[i][j] = INF;
				dpx[i][j] = -INF;
				for (int k = i; k < j; k++) {
					dpm[i][j] = min(dpm[i][j], dpm[i][k] + dpm[k + 1][j] + sum[j] - sum[i - 1]);
					dpx[i][j] = max(dpx[i][j], dpx[i][k] + dpx[k + 1][j] + sum[j] - sum[i - 1]);
				}
			}
		}
	}

	// 遍历所有起点取最优解
	int min_ans = INF, max_ans = -INF;
	for (int i = 1; i <= n; i++) {
		min_ans = min(min_ans, dpm[i][i + n - 1]);
		max_ans = max(max_ans, dpx[i][i + n - 1]);
	}
	cout << min_ans << endl << max_ans;
	return 0;
}

P3146 [USACO16OPEN] 248 G

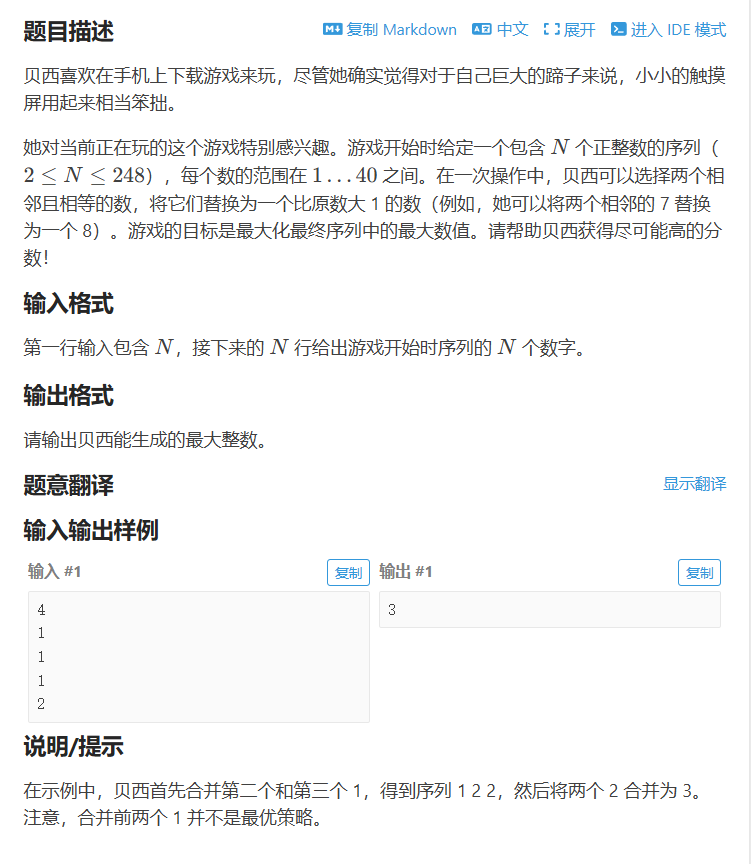
#include <bits/stdc++.h>
using namespace std;

int n;
int arr[255], dp[255][255],ans=0;

int main() {
	cin >> n ;
	for (int i = 1; i <= n; i++) {
		cin >> arr[i];
	}
	for (int k = 1; k <= n; k++) {
		for (int i = 1; i + k - 1 <= n; i++) {
			if (k == 1) {
				dp[i][i + k - 1] = arr[i];
				ans=max(ans,arr[i]);
			} else {
				for (int j = i; j < i + k - 1; j++) {
					if (dp[i][j] == dp[j+1][i + k - 1]&&dp[i][j]) {
						dp[i][i + k - 1] = max(dp[i][i + k - 1], dp[i][j] + 1);
						ans=max(ans,dp[i][i+k-1]);
					}
				}
			}
		}
	}
	cout << ans;
	return 0;
}

P1063 [NOIP 2006 提高组] 能量项链

首先是一道环形的题，因此对环形进行处理，在原数据数组基础上复制一份，动态规划的时候都要一起更新，最后从1到n进行长度为n的遍历，找到最大值。

用pair<int,int> arr数组记录每个数据的头和尾。动态规划时，遍历j，找到 i到i+len-1的最大值：i到j的最大值加上j+1到i+len-1的最大值加上三个数相乘 的最大值。AC代码如下：

#include <bits/stdc++.h>
using namespace std;

int n;
pair<int, int> arr[205];
int dp[205][205];

int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		if (i == 1) {
			cin >> arr[i].first >> arr[i].second;
		} else if (i == n) {
			arr[i].first = arr[i - 1].second;
			arr[i].second = arr[1].first;
		} else {
			cin >> arr[i].second;
			arr[i].first = arr[i - 1].second;
		}
		arr[i + n].first = arr[i].first;
		arr[i + n].second = arr[i].second;

	}
	for (int i = 1; i <= 2 * n; i++) {
		dp[i][i] = 0;
	}
	for (int len = 2; len <= n; len++) {
		for (int i = 1; i + len - 1 <= 2 * n; i++) {
			for (int j = i; j < i + len - 1; j++) {
				dp[i][i + len - 1] = max(dp[i][i + len - 1],
				                         dp[i][j] + dp[j + 1][i + len - 1] + arr[i].first * arr[j].second * arr[i + len - 1].second);
			}
		}
	}
	int ans = 0;
	for (int i = 1; i <= n; i++) {
		ans = max(ans, dp[i][i + n - 1]);
	}
	cout << ans;
	return 0;
}

P1005 [NOIP 2007 提高组] 矩阵取数游戏

学了一手__int128 的用法

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int n, m;
int arr[85];
__int128 dp[85][85], ans;

void out (__int128 x) {
	if (x > 9)
		out(x / 10);
	putchar(x % 10 + '0');
}

int main() {
	cin >> n >> m;
	int t = n;
	while (t--) {
		memset(dp, 0, sizeof(dp));
		for (int i = 1; i <= m; i++) {
			cin >> arr[i];
			dp[i][i] = 2 * arr[i];
		}
		for (int len = 2; len <= m; len++) {
			for (int i = 1; i + len - 1 <= m; i++) {
				int j = i + len - 1;
				for (int k = i; k < j; k++) {
					dp[i][j] = max(dp[i + 1][j] + arr[i], dp[i][j - 1] + arr[j]) * 2;
				}
			}
		}
		ans += dp[1][m];
	}
	out(ans);
	return 0;
}

P4170 [CQOI2007] 涂色

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

string s;
char tar[55];
int dp[55][55], ans;

int main() {
	cin >> s;
	int sz = s.size();
	for (int i = 1; i <= sz; i++) {
		dp[i][i] = 1;
		tar[i] = s[i - 1];
	}

	for (int len = 2; len <= sz; len++) {
		for (int i = 1; i + len - 1 <= sz; i++) {
			int j = i + len - 1;
			if (tar[i] == tar[j]) {
				dp[i][j] = dp[i][j - 1];
			} else {
				dp[i][j] = dp[i][i] + dp[i + 1][j];
				for (int k = i; k < j; k++) {
					dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j]);
				}
			}
		}
	}
	cout << dp[1][sz];
	return 0;
}

P4302 [SCOI2003] 字符串折叠

#include <bits/stdc++.h>
using namespace std;
string st;
int n, m[110], f[110][110];

bool check(int l, int r, int len) {
	for (int i = l; i <= r; i++)
		if (st[i] != st[(i - l) % len + l])
			return false;
	return true;
}

int main() {
	cin >> st;
	n = st.size();
	st = ' ' + st;
	for (int i = 1; i <= 9; i++)
		m[i] = 1;
	for (int i = 10; i <= 99; i++)
		m[i] = 2;
	m[100] = 3;
	memset(f, 0x3f, sizeof(f));
	for (int i = 1; i <= n; i++)
		f[i][i] = 1;
	for (int l = 2; l <= n; l++) {
		for (int i = 1, j = i + l - 1; j <= n; i++, j++) {
			for (int k = i; k < j; k++)
				f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j]);
			for (int k = i; k < j; k++) {
				int len = k - i + 1;
				if (l % len != 0)
					continue;
				if (check(i, j, len))
					f[i][j] = min(f[i][j], f[i][k] + 2 + m[l / len]);
			}
		}
	}
	printf("%d", f[1][n]);
	return 0;
}

P2466 [SDOI2008] Sue 的小球

简单讲一下我的思考过程：这还是一道区间dp，最开始想的是让dp[i][j]表示第i个到第j个区间得分最大值。但是，怎么合并区间呢，或者说怎么推到下一个区间呢？发现好像没有很好的办法，因为并不知道是从什么时候到这个区间的，不知道此时的时间，自然就无法知道得分。

可以考虑用dp[i][j]表示从i到j这个区间的过程中，其它区间最少会浪费多少积分。f[i][j]表示当处于i点时，经过了i到j浪费的最少积分；g[i][j]表示处于j点时浪费的积分。初始位置为x，则f[x][x]=g[x][x]=0。

#include <bits/stdc++.h>
using namespace std;
#define MAXN 1005
#define rg register
struct zjy{
    int x,y,v;
}ball[MAXN];
int f[MAXN][MAXN],g[MAXN][MAXN],tot;
int x0,n,pre[MAXN];
bool cmp(zjy x,zjy y){return x.x<y.x;}
int js(int l,int r){return pre[r]-pre[l-1];}
int main(){
    memset(f,0x3f,sizeof(f));
    memset(g,0x3f,sizeof(g));
    ios::sync_with_stdio(false);
    cin>>n>>x0;
    for(rg int i=1;i<=n;++i)cin>>ball[i].x;
    for(rg int i=1;i<=n;++i)cin>>ball[i].y,tot+=ball[i].y;
    for(rg int i=1;i<=n;++i)cin>>ball[i].v;
    ball[++n].x=x0;
    sort(ball+1,ball+n+1,cmp);
    for(rg int i=1;i<=n;++i)pre[i]=pre[i-1]+ball[i].v;
    for(rg int i=1;i<=n;++i)if(ball[i].v==0&&ball[i].x==x0)f[i][i]=0,g[i][i]=0;
    for(rg int k=1;k<n;++k)for(rg int i=1,j=i+k;i<=n&&j<=n;++i,j=i+k){
        f[i][j]=min(f[i][j],f[i+1][j]+(js(1,i)+js(j+1,n))*(ball[i+1].x-ball[i].x));
        f[i][j]=min(f[i][j],g[i+1][j]+(js(1,i)+js(j+1,n))*(ball[j].x-ball[i].x));
        g[i][j]=min(g[i][j],g[i][j-1]+(js(1,i-1)+js(j,n))*(ball[j].x-ball[j-1].x));
        g[i][j]=min(g[i][j],f[i][j-1]+(js(1,i-1)+js(j,n))*(ball[j].x-ball[i].x));
    }
    printf("%.3lf",(tot-min(f[1][n],g[1][n]))/1000.0);
}

Part4 树形动态规划

树形动态规划，即在树上进行的动态规划。因为树的递归性质，树形动态规划一般都是递归求解的。

P1352 没有上司的舞会

一道经典的树形dp。

#include <bits/stdc++.h>
using namespace std;

int n, v[6005], syb[6005], root, dp[6005][2];
vector<int> son[6005];

void dfs(int x) {
	dp[x][0] = 0;
	dp[x][1] = v[x];
	for (int i = 0; i < son[x].size(); i++) {
		int tar = son[x][i];
		dfs(tar);
		dp[x][0] += max(dp[tar][0], dp[tar][1]);
		dp[x][1] += dp[tar][0];
	}
	return;
}

int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> v[i];
	}
	int temp1, temp2;
	for (int i = 1; i <= n - 1; i++) {
		cin >> temp1 >> temp2;
		son[temp2].push_back(temp1);
		syb[temp1] = 1;
	}
	for (int i = 1; i <= n; i++) {
		if (!syb[i]) {
			root = i;
			break;
		}
	}
	dfs(root);
	cout << max(dp[root][0], dp[root][1]);
	return 0;
}

P1122 最大子树和

题目背景的意思，其实本质上已经在题目这行显示了：最大子树和。这道题并不是二叉树，也没有指明左边还是右边是父节点，因此默认左边是子节点，右边是父节点，但是这样一来就会有很多“根节点”。因此需要对“多个根节点”进行处理

#include <bits/stdc++.h>
using namespace std;

int n, v[16005], syb[16005], ans = -0x3f3f3f, dp[16005];
vector<int> son[16005];
vector<int> root;

void dfs(int x) {
	dp[x] = v[x];
	for (int i = 0; i < son[x].size(); i++) {
		int tar = son[x][i];
		dfs(tar);
		if (dp[tar] >= 0) {
			dp[x] += dp[tar];
		}
	}
	return;
}



int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> v[i];
		ans = max(ans, v[i]);
	}
	int x, y;
	for (int i = 1; i <= n - 1; i++) {
		cin >> x >> y;
		son[y].push_back(x);
		syb[x] = 1;
	}
	for (int i = 1; i <= n; i++) {
		if (!syb[i]) {
			root.push_back(i);
		}
	}
	int temp;
	for (int i = 0; i < root.size(); i++) {
		dfs(root[i]);
		ans = max(ans, dp[root[i]]);
		if (ans == dp[root[i]]) {
			temp = i;
		}
	}
	for (int i = 1; i < root.size(); i++) {
		if (i == temp) {
			continue;
		}
		if (v[i] < 0) {
			continue;
		}
		ans += v[i];
	}


	if (ans < 0) {
		for (int i = 1; i <= n; i++) {
			ans = max(ans, dp[i]);
		}
	}
	cout << ans;
	return 0;
}

P1040 [NOIP 2003 提高组] 加分二叉树